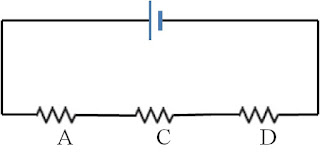
Question: 4. A circuit contains a battery and four identical resistors arranged as shown in the diagram below.
(a) Rank the electrical potential difference across each resistor in descending order. If any resistors have potential differences with the same magnitude, state that explicitly. Explain your answer.
(b) When resistor B is removed in the electrical circuit, what happens to the electric current through resistor A? Explain your answer.
(c) When resistor B is removed in the electrical circuit, what happens to the electric current through resistor C? Explain your answer.
Scoring Guidelines:
(a) Ranking: RA = RD > RB = RC.
Indicate that the electrical potential difference is the same in RA and RD because the electric current is the same through RA and RD. [1 mark]
Indicate that the electrical potential difference is the same in RB and RC because RB and RC are in parallel. [1 mark]
Indicate that the electrical potential difference is less in RB (and/or RC) than in RA (and/or RD) because the electric current splits through RB and RC. [1 mark]
(b) Indicate that the effective resistance of the circuit increases. [1 mark]
Explain correctly why the electric current through RA decreases because of the change in electric current or electrical potential difference in the circuit. [1 mark]
(c) Indicate that the electric current through the battery is the same as electric current through RC and there is no splitting of electric current. [1 mark]
(https://secure-media.collegeboard.org/digitalServices/pdf/ap/apcentral/ap16_physics_1_q4.pdf)
(https://secure-media.collegeboard.org/digitalServices/pdf/ap/apcentral/ap16_physics_1_q4.pdf)
Possible answers:
The electrical circuit can be redrawn as follows;
(a) Let the electromotive force of the battery be E and the resistance of each resistor be r. Total resistance = RA + RB,C + RD = r + r/2 + r = 5r/2.
By using Ohm’s law, I = V/R = E/(5r/2) = (2/5)(E/r) = 0.40 (E/r).
Thus, ΔVA = ΔVD = Ir = 0.40 E and ΔVB = ΔVC = 0.20 E.
The ranking of electrical potential difference can be presented as follows:
ΔVA = ΔVD > ΔVB = ΔVC.
(b) After removing the resistor B, the electrical circuit can be redrawn as follows:
Total resistance = RA + RC + RD = r + r + r = 3r.
Electric current, Ia = V/R = E/3r = 0.33 (E/r).
The electric current is decreased from 0.40 (E/r) to 0.33 (E/r).
Thus, the answer is “decrease.”
(c) The electric current through resistor C also equals to 0.33 (E/r) because the three resistors A, B, and C are in series and have the same resistance r.
However, the electric current through resistor C in the original circuit is IA/2 = 0.20 (E/r) because the electric current through resistor A is equally split in resistor C and resistor B.
The electric current is increased from 0.20 (E/r) to 0.33 (E/r).
Thus, the answer is “increase.”
Feynman’s insights or goofs?:
In Feynman’s own words, “[t]he second kind of circuit element is called a resistor; it offers resistance to the flow of electrical current. It turns out that metallic wires and many other substances resist the flow of electricity in this manner: if there is a voltage difference across a piece of some substance, there exists an electric current I = dq/dt that is proportional to the electric voltage difference: V = RI = Rdq/dt. The proportionality coefficient is called the resistance R. This relationship may already be familiar to you; it is Ohm’s law (Feynman et al., 1963, section 23–3 Electrical resonance).” Essentially, Feynman explains that Ohm’s law is about the mathematical relationship, V = RI = Rdq/dt. However, some physics educators may not like the phrase “flow of electric current” as used by Feynman. This is because electric current is a flow of charge carriers and thus, the flow of electric current is “the flow of flow of charge carriers.”
In his Nobel lecture, Wilczek (2004) humorously says that “Ohm’s first law is V = IR. Ohm’s second law is I = V/R. I’ll leave it to you to reconstruct Ohm’s third law (p. 413).” Historically speaking, there are at least two different versions of Ohm’s Law: ‘the law for a part of a circuit’ and ‘the law for a whole circuit’ (Ashford and Kempson 1908; Kipnis 2009). Ohm’s law for a part of a circuit means that an electric current through an electrical conductor is directly proportional to the potential difference across the conductor, and the resistance of the conductor is assumed to be constant. This version of Ohm’s law can be represented by the equation, I = ΔV/R. Alternatively, Ohm’s law for a whole circuit means that an electric current through a conductor is directly proportional to the potential difference across the conductor and it is inversely proportional to its resistance. This version of Ohm’s laws can be represented by the following equation, I = E/(R + r), in which E is the electromotive force of a power supply and r is the internal resistance of the power supply.
To be more precise, Ohm’s law can be defined by stating the operating conditions such as the electric current is not too high. When the electrical current is sufficiently high, this can lead to a significant heating effect. First, a heating of the electrical conductor may increase the temperature of the conductor. Second, the increase in temperature can result in an increase in the length of the conductor. Third, when the temperature of the conductor is being increased, the electrical resistance is also increased, and this can lead to a reduction in the electric current through the conductor. Thus, Ohm’s law does not always hold because electrical properties of the conductor are dependent on the operating conditions.
In his Nobel lecture, Wilczek (2004) humorously says that “Ohm’s first law is V = IR. Ohm’s second law is I = V/R. I’ll leave it to you to reconstruct Ohm’s third law (p. 413).” Historically speaking, there are at least two different versions of Ohm’s Law: ‘the law for a part of a circuit’ and ‘the law for a whole circuit’ (Ashford and Kempson 1908; Kipnis 2009). Ohm’s law for a part of a circuit means that an electric current through an electrical conductor is directly proportional to the potential difference across the conductor, and the resistance of the conductor is assumed to be constant. This version of Ohm’s law can be represented by the equation, I = ΔV/R. Alternatively, Ohm’s law for a whole circuit means that an electric current through a conductor is directly proportional to the potential difference across the conductor and it is inversely proportional to its resistance. This version of Ohm’s laws can be represented by the following equation, I = E/(R + r), in which E is the electromotive force of a power supply and r is the internal resistance of the power supply.
To be more precise, Ohm’s law can be defined by stating the operating conditions such as the electric current is not too high. When the electrical current is sufficiently high, this can lead to a significant heating effect. First, a heating of the electrical conductor may increase the temperature of the conductor. Second, the increase in temperature can result in an increase in the length of the conductor. Third, when the temperature of the conductor is being increased, the electrical resistance is also increased, and this can lead to a reduction in the electric current through the conductor. Thus, Ohm’s law does not always hold because electrical properties of the conductor are dependent on the operating conditions.
References:
1. Ashford, C. E., & Kempson, E. W. E. (1908). The elementary theory of direct current dynamo electric machinery. Cambridge: The University Press.
2. Feynman, R. P., Leighton, R. B., & Sands, M. (1963). The Feynman Lectures on Physics, Vol I: Mainly mechanics, radiation, and heat. Reading, MA: Addison-Wesley.
3. Kipnis, N. (2009). A Law of Physics in the Classroom: The Case of Ohm’s Law. Science & Education, 18(3-4), 349-382.
4. Wilczek, F. (2004). Asymptotic freedom: From Paradox to Paradigm. In F., Wilczek, & B., Devine, (Eds.). (2006). Fantastic Realities: 49 Mind Journeys and a Trip to Stockholm. Singapore: World Scientific.


Queen of Spades | Shootercasino
ReplyDeleteQueen of Spades In classic Blackjack 제왕 카지노 this is the queen of spades. This 카지노사이트 is where I play this game. Aces are drawn as they 바카라 roll. I have four in total