AP Physics 1 2017 Free Response Question 2

Question:

(a) Students are required to propose an experiment for determining the coefficient of static friction between a small wooden block and a flat wooden board. 

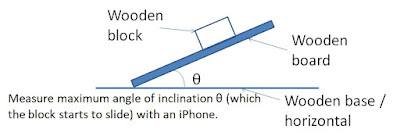
(i) Sketch a diagram that illustrates the experiment and indicate the measured quantity. The equipment that is used for measurement should be stated or drawn. 

(ii) Outline the procedure with details such that another student could perform the same experiment. 

(b) Students derive an equation of static friction in terms of measured quantities that are stated in the experimental procedure mentioned earlier. 

(c) Six lab groups perform the same experiment to test the hypothesis that the coefficient of static friction between the wooden board and the wooden block is equal to the coefficient of kinetic friction for the same materials.

The results of coefficient of kinetic friction determined by 6 groups (GP) of students are summarised as follows: 0.45 (GP 1), 0.46 (GP 2), 0.42 (GP 3), 0.43 (GP 4), 0.74 (GP 5), 0.44 (GP 6) and the average is 0.49. 

The results of coefficient of static friction are summarised as follows: 0.54 (GP 1), 0.52 (GP 2), 0.56 (GP 3), 0.55 (GP 4), 0.23 (GP 5), 0.54 (GP 6) and the average is also 0.49. 

Based on these experimental data, students need to conclude and justify whether the coefficient of static friction is equal to the coefficient of kinetic friction. (d) The wooden block is glued to a metal disk such that the mass of the block-disk system is two times the mass of the wooden block. Students need to give their reasoning on whether the coefficient of static friction between the bottom of the wooden block and the wooden board is increased, decreased, or remain unchanged.

Possible answers: 

1 (a) (i) A simple experiment to determine the coefficient of friction is represented below. The angle of tilt of the wooden board can be measured by using an inclined plane apparatus with a protractor (or an iPhone). 

(ii) Place a wooden board on a wooden inclined plane. Students slowly increase the inclination angle of the board until the wooden block just begins to slide. Measure the maximum angle of inclination between the inclined plane and the horizontal. Repeat the experiment by placing the block at different locations on the board. (Nowadays, students may use an iPhone as a protractor to measure the maximum angle of inclination in which the wooden block just begins to move.) Alternatively, the sliding motion of the wooden block may be confirmed by a motion detector. 

(b) Resolving forces parallel to the inclined plane: 

mg sin θ - m_sN = 0 Þ mg sin θ = m_sN --- --- Equation (1). 

Resolving forces perpendicular to the inclined plane: 

mg cos θ - N = 0 Þ mg cos θ = N --- --- Equation (2). 

Dividing Equation (1) by Equation (2) gives: mg sin θ / mg cos θ = m_sN / N Þ tan θ = m_s   in which θ is the maximum angle of inclination. 

(c) One possible answer is the coefficient of static friction (m_s) is not exactly equal to the coefficient of kinetic friction (m_k). A possible reason: the experimental result of group 5 is an outlier, and thus, it can be excluded. However, the coefficient of static friction of wood may vary approximately from 0.25 to 0.50 depending on the type of wood used (Aira, Arriaga, Íñiguez-González, & Crespo 2014). Strictly speaking, the experimental result of group 5 is not necessarily due to an incorrect experimental procedure. In general, it is not definitely correct to drop a group’s observations and regard them to be an outlier. 

(d) One may select the answer “remain the same” and explain that the coefficient of static friction depends on the nature of the surfaces instead of the total mass of the block-disk system or the normal force on the object. However, the coefficient of static friction may be increased or decreased depending on the initial roughness of the surface of the wooden block and the wooden board. In general, the coefficient of static friction varies from 0.7 to 0.9 if the surface of the wood is wet instead of dry (Glass & Zelinka, 2010).

Feynman’s insights or goofs?: 

(a) In Feynman’s own words, “the formula F = μN is approximately correct can be demonstrated by a simple experiment. We set up a plane, inclined at a small angle θ, and place a block of weight W on the plane. We then tilt the plane at a steeper angle, until the block just begins to slide from its own weight (Feynman et al., 1963, section 12-2 Friction).” Interestingly, we can now use a smartphone (or iPhone) to measure the angle of inclination more accurately by downloading an App. If students have sweaty palms, they should use a pair of gloves such that the coefficient of friction does not increase (due to moisture absorption). 

(b) One may quote Feynman’s words in deriving an equation of static friction, “[t]he component of the weight downward along the plane is W sin θ, and this must equal the frictional force F when the block is sliding uniformly. The component of the weight normal to the plane is W cos θ, and this is the normal force N. With these values, the formula becomes W sin θ = μW cos θ, from which we get μ = sin θ / cos θ = tan θ. If this law were exactly true, an object would start to slide at some definite inclination (Feynman et al., 1963, section 12-2 Friction).” Note that all experimental data can fit into the equation μ = tan θ, but the coefficient of static friction for wood, for example, is not a definite value and can vary from 0.25 to 0.50 (Aira, Arriaga, Íñiguez-González, & Crespo 2014).

Physics teachers may explain that the equation μ = tan θ is merely a mathematical relationship instead of describing it as a law. Historically speaking, there are two laws of static friction: (1) the static frictional force (F) is proportional to the normal reaction (N) and can be represented as F = μ_sN (Amontons’ first law). (2) the static frictional force is independent of the apparent area of contact (Amontons’ second law). On the other hand, there is a law of kinetic friction: the kinetic frictional force is independent of sliding speed (Coulomb’s law). Importantly, these empirical laws have limited conditions of applicability because frictional forces are rather complex. In general, frictional forces are influenced by many factors such as surface cleanliness, surface roughness, contact temperature, relative humidity, and presence of loose particles (Blau, 2008). 

(c) In a sense, Feynman might disagree with asking the question whether the coefficient of static friction is equal to the coefficient of kinetic friction. His argument can be found in his lecture on friction: “It is quite difficult to do accurate quantitative experiments in friction, and the laws of friction are still not analyzed very well, in spite of the enormous engineering value of an accurate analysis. Although the law F = μN is fairly accurate once the surfaces are standardized, the reason for this form of the law is not really understood. To show that the coefficient μ is nearly independent of velocity requires some delicate experimentation because the apparent friction is much reduced if the lower surface vibrates very fast. When the experiment is done at very high speed, care must be taken that the objects do not vibrate relative to one another, since apparent decreases of the friction at high speed are often due to vibrations. At any rate, this friction law is another of those semi-empirical laws that are not thoroughly understood, and in view of all the work that has been done it is surprising that more understanding of this phenomenon has not come about (Feynman et al., 1963, section 12-2 Friction).” 

(d) In the last part of the question, if you select “remain the same”, you may quote the following statements of Feynman: “If the same block is loaded by putting extra weight on it, then, although W is increased, all the forces in the formula are increased in the same proportion, and W cancels out. If μ stays constant, the loaded block will slide again at the same slope. When the angle θ is determined by trial with the original weight, it is found that with the greater weight the block will slide at about the same angle. This will be true even when one weight is many times as great as the other, and so we conclude that the coefficient of friction is independent of the weight (Feynman et al., 1963, section 12-2 Friction).” One should recognize that Feynman mentions a condition: “if μ stays constant”. Of course, this is an idealization because frictional forces are dependent on many other factors, as mentioned earlier. 

Alternatively, if you select “increase”, you may argue that it does not remain the same by quoting the following statement of Feynman: “[i]f the normal force or the speed of motion gets too big, the law fails because of the excessive heat generated (Feynman et al., 1963, section 12-2 Friction).” This is also a possible option because of the complex nature of frictional forces. To be more accurate, the frictional force can be represented by the relation F = μN + kA where kA indicates that it is proportional to the area of contact between two surfaces (Besson, Borghi, De Ambrosis, & Mascheretti, 2007).

References: 1. Aira, J. R., Arriaga, F., Íñiguez-González, G., & Crespo, J. (2014). Static and kinetic friction coefficients of Scots pine (Pinus sylvestris L.), parallel and perpendicular to grain direction. Materiales de Construcción, 64(315), 030. 
2. Besson, U., Borghi, L., De Ambrosis, A., & Mascheretti, P. (2007). How to teach friction: Experiments and models. American Journal of Physics, 75(12), 1106-1113. 
3. Blau, P. J. (2008). Friction science and technology: from concepts to applications (2nd ed.). Boca Raton: CRC Press. 
4. Feynman, R. P., Leighton, R. B., & Sands, M. (1963). The Feynman Lectures on Physics, Vol I: Mainly mechanics, radiation, and heat. Reading, MA: Addison-Wesley. 
5. Glass, S. V., & Zelinka, S. L. (2010). Moisture relations and physical properties of wood. In R. J. Ross (ed.) Wood handbook: wood as an engineering material: chapter 4. Centennial ed. General technical report FPL; GTR-190. Madison, WI: US Dept. of Agriculture, Forest Service, Forest Products Laboratory (pp. 4.1-4.19).